In the realm of structural engineering, the ability to predict and analyze how structures respond to external forces is crucial. Modal analysis is a sophisticated technique that provides deep insights into the dynamic behavior of structures. It plays a vital role in identifying natural frequencies, mode shapes, and damping characteristics, which are essential for designing robust and resilient structures. This blog post delves into the fundamental concepts of modal analysis.
The Essence of Modal Analysis: At its core, modal analysis is about understanding how structures vibrate. Every structure, whether it’s a towering skyscraper or a simple bridge, has specific frequencies at which it naturally tends to vibrate. These are known as the natural frequencies. When an external force matches one of these frequencies, resonance occurs, potentially leading to significant and often undesirable vibrations.

Natural Frequency and Resonance: Natural frequencies are inherent to the structure’s material properties and geometry. Resonance, on the other hand, is a powerful phenomenon where a structure, subjected to a dynamic force at its natural frequency, experiences amplified vibrations. This can range from minor annoyances, like a vibrating steering wheel, to severe outcomes such as the catastrophic failure of an airplane wing.
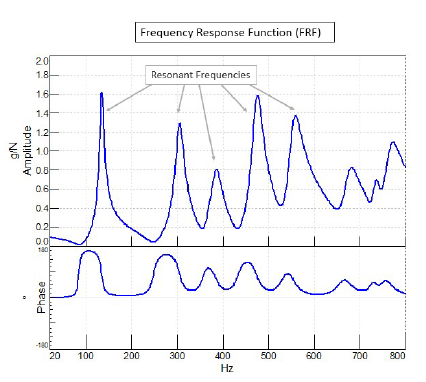
Exploring the Frequency Response Function (FRF): The Frequency Response Function (FRF) is a cornerstone of modal analysis. It characterizes the frequency domain relationship between an input force and the resulting output response of a structure. By plotting the FRF, engineers can pinpoint the resonant frequencies, observe the damping effects, and understand the mode shapes. Peaks in the FRF indicate natural frequencies, while the width of these peaks reflects the damping level.
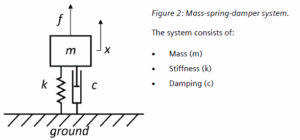
Single Degree of Freedom (SDOF) Systems: One of the simplest models in modal analysis is the Single Degree of Freedom (SDOF) system. This model, consisting of a mass-spring-damper system, provides foundational insights into how changes in mass or stiffness can influence a system’s natural frequency. It serves as a microcosm of more complex real-world structures, offering a clear picture of resonant behavior.
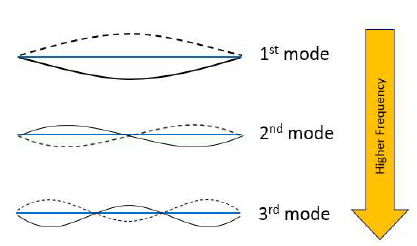
Deciphering Mode Shapes and Damping: Mode shapes illustrate how different parts of a structure move at each natural frequency. Understanding these shapes is pivotal for engineers, as it helps identify potential weaknesses or areas requiring reinforcement. Damping, the mechanism by which a system dissipates vibrational energy, is equally critical. It determines how swiftly vibrations subside, influencing the overall stability and comfort of the structure.
Strategies for Mitigating Resonance: Resonance, while fascinating, can be destructive. Engineers deploy various strategies to counteract its effects. Modifying mass and stiffness, enhancing damping, or implementing tuned absorbers are common approaches. For instance, altering the mass or stiffness of a guitar string changes its natural frequency, providing an intuitive analogy for structural modifications.
Real-World Applications: Modal analysis is not confined to theoretical exercises; its applications are vast and varied. In the automotive industry, it aids in reducing noise and improving ride comfort. In aerospace, it is pivotal for ensuring the safety and performance of aircraft. Civil engineers use it to design earthquake-resistant buildings and bridges, optimizing them for dynamic loads.

Conclusion: Modal analysis is an indispensable tool in the toolkit of modern engineers. By unlocking the secrets of structural dynamics, it enables the design of safer, more efficient, and more reliable structures. Whether it’s preventing catastrophic failures or enhancing everyday comfort, modal analysis provides the insights needed to innovate and improve. For those seeking a deeper understanding, Siemens’ “Modal Analysis – Knowledge Booklet” offers a comprehensive guide, rich with technical details and practical applications, illuminating the path to mastering this essential discipline.